|
Click here for PDF version (no pictures yet, but the formatting's
better).
This paper copyright 1991 by Kevin Gong.
Please forgive the formatting. I'll try to fix it at some later
date. I'll also add the illustrations later.
Case Study:
Applying Parallel Programming to the Polyomino Problem
Kevin Gong
UC Berkeley
CS 199 Fall 1991
Faculty Advisor:
Professor Katherine Yelick
Acknowledgements
Thanks to Martin Gardner, for introducing me to polyominoes (and
a host
of other problems).
Thanks to my faculty advisor, Professor Katherine Yelick.
Parallel runs for this project were performed on a 12-processor
Sequent machine.
Sequential runs were performed on Mammoth. This machine was purchased
under an NSF CER infrastructure grant, as part of the Mammoth
project.
Format
This paper was printed on a Laserwriter II using an Apple Macintosh
SE running Microsoft Word. Section headings and tables are printed
in Times font. The text itself is printed in Palatino font. Headers
and footers are in Helvetica.
Contents
1 Introduction
2 Problem
3 Existing Research
4 Sequential Enumeration
- 1 Extension Method
- 1.1 Generating Polyominoes
- 1.2 Hashing
- 1.3 Storing Polyominoes For Uniqueness Check
- 1.4 Data Structures
- 2 Rooted Translation Method
- 2.1 Tree Growth: Breadth-First vs. Depth-First
- 2.2 3-Dimensional Polyominoes
- 3 Performance Comparison
- 3.1 Hash Structure Performance
- 3.2 Extension vs. Move-List
- 3.3 Extension Method
- 3.4 Rooted Method
- 3.5 3-Dimensional Polyominoes
5 Parallel Enumeration
- 1 Extension Method
- 1.1 Locking the Hash Structure
- 1.2 Announcement Board
- 2 Rooted Translation Method
- 2.1 3-Dimensional Polyominoes
- 3 Performance Comparison
- 3.1 Extension Method
- 3.2 Rooted Method
- 3.3 3-Dimensional Polyominoes
6 Results
7 Conclusion
8 References
Illustrations
Appendix A - Evaluation of Hash Functions
Appendix B - Exact Times
Appendix C - Program Listings
1 Introduction
Parallel programming is a growing field of study. Recently, parallel
programming helped solve an ancient chess problem -- proving that
a king, rook, and bishop can defeat a king and two knights in
223 moves. This amazing feat, directed by Lewis Stiller at Johns
Hopkins University, was accomplished by using 65,536 processors
to analyze 100 billion moves by retrograde analysis (starting
from a won position and working backwards). [SFC91]
Parallel programming allows us to increase computing power even
without more powerful chips. Effectively using 10 computer chips
together is just as good as improving a single chip to allow 10
times the performance. Doing both, of course, would be even better.
We will explore some of the problems that parallel programming
presents by exploring its usefulness in solving a single problem.
First, we will
present a sequential solution, then consider some of the problems
involved as we create a parallel solution.
We will begin with a thorough definition of the problem.
2 Problem
To demonstrate some of the concerns of parallel programming, we
will consider the problem of enumerating polyominoes.
Polyominoes are the creation of Solomon Golomb, and are described
in his book so entitled. [Gol65]
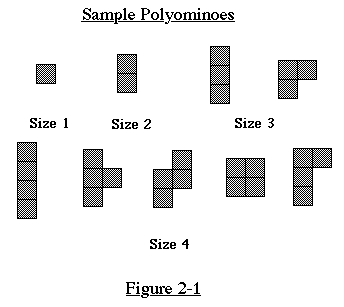
A polyomino (pol-e-AHM-ih-no, as in 'domino') is a connected collection
of squares. The squares must be placed as if on a grid (they cannot
be staggered). A polyomino of size n is one with exactly n squares.
See Figure 2-1 for examples of polyominoes.
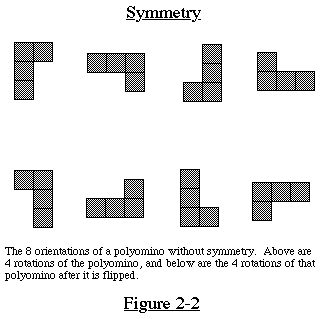
In enumerating the polyominoes, we do not count translations,
rotations, or reflections of the same polyomino. Ignoring translation,
any polyomino has at most 8 different orientations, only one of
which is counted. If a polyomino has no symmetry, it can be rotated
to form 4 different orientations, then flipped over and rotated
again to form the other 4 orientations. See Figure 2-2 for an
illustration of this. The flipping over is equivalent (modulo
rotation) to reflection along any axis.
The problem is to find the number of polyominoes of any given
size. For example, there are exactly 12 polyominoes of size 5.
We will find it useful to use the notion of linesize. A polyomino
has linesize m if it contains a straight line of m consecutive
squares, and there is no such line with more than m squares. See
Figure 2-3 for an illustration of this concept.
3-Dimensional Polyominoes
An extension of this problem is to enumerate the number of 3-dimensional
polyominoes of any size. A 3-dimensional polyomino is a connected
collection of cubes. See Figure 2-4 for some examples.
In enumerating 3-dimensional polyominoes, we must decide which
ones are the same and should not be counted again. This is a little
unclear. Note that in the 2-dimensional case, we perform a 3-dimensional
transformation (reflection in 2-dimensions is equivalent to rotation
in 3 dimensions). So, should we allow a 4-dimensional transformation
when enumerating 3-dimensional polyominoes? One could argue either
way, so we will do both.
In enumerating the 3-dimensional rotation polyominoes, we do not
count translations or rotations of the same polyomino. A polyomino
without symmetry has 24 different orientations. This is easy to
visualize with a die or Rubik's cube. A die has 6 faces numbered
1 thru 6. If we place a die on the table with the '1' showing
up, we can rotate it to get 4 different orientations with the
1 still on top. Since there are 6 faces, there are 6x4 = 24 different
orientations. Another way to look at it is this: A cube has 12
edges. If we look at a single edge in space, any of those edges
can occupy that space, and there are 2 different orientations
for each, so there are 2x12 = 24 different orientations.
In enumerating the 3-dimensional reflection polyominoes, we do
not count translations, rotations, or reflections of the same
polyomino. A polyomino without symmetry has 48 different orientations.
This is similar to the 2-dimensional case in that we simply reflect
the polyomino to get 2 times as many orientations (2x24 = 48).
Some careful thought will convince the reader that reflections
along any axis are equivalent modulo rotation.
3 Existing Research
Much research has been done on the problem of enumerating polyominoes.
Formulas have been found for special cases of polyominoes, but
the main
problem remains an open one.
Polyominoes have been discussed by Gardner [Gar59], and are popular
in different forms of puzzles.
The problem is also known as the cell growth problem and polyominoes
are sometimes called 'animals'. [Rea62]
According to Delest, enumeration of polyominoes is a major unsolved
problem. A huge number of asymptotic results has been given by
physicists
for whom such objects are important in statistical mechanics.
[Del84]
Most recently, Delest has compiled a table summarizing the asymptotic
and exact results of different subsets of polyominoes, and provides
references to articles on these results. [Del91]
Enumeration
Dudeney noted the 12 pentominoes (size 5 polyominoes) before 1919.
The values for up to size 6 were known since at least 1937. [Mad69]
According to Read, values for 7 and 8 were computed by MANIAC
II
at Los Alamos in 1959. In 1962, Read calculated the number of
size 9 polyominoes, but incorrectly calculated the number of size
10 polyominoes (as 4466). Read used methods to calculate the number
of polyominoes which fit in rectangles of certain sizes. [Rea62]
In 1967, David A. Klarner listed the values for up to size 12.
[Kla67]
Also in 1967, T.R. Parkin and others calculated the number of
polyominoes up to size 15. [Par67] This was accomplished using
a CDC 6600. Their figure for size 15, however, was incorrect (figures
for sizes up to 14 were correct).
In 1971, Lunnon calculated the values for up to size 18. [Lun71]
This was accomplished on an Atlas I running a program for 175
hours. The figures are claimed to be correct to within a few hundred.
Any errors are blamed on hardware errors. The value for 17 was
incorrect (it is off by 2).
By 1981, D.H. Redelmeier calculated for up to size 24. [Kla81]
All the numbers match Lunnon's enumeration except for 17 (it is
assumed that Lunnon was incorrect). (See Figure 3-1)
In 1972, Lunnon calculated by hand the number of 3-dimensional
polyominoes up to size 6. (See Figure 3-2) [Lun72]

Lunnon also calculated some values for triangular and hexagonal
polyominoes (using triangles and hexagons instead of squares).
[Lun72-2]
Asymptotic Growth
Klarner has proven that the asymptotic growth of p(n), the number
of polyominoes of size n, is theta^n. [Kla81] He proves that:
3.72 < theta < 4.65. He also shows that the lower bound can be
raised if values of p(n) for larger n are known.
Because of this result, any program which enumerates polyominoes
(without skipping classes of polyominoes) cannot run in polynomial
time. So, the challenge is to write a program which runs in k*p(n)
time, where k is
a constant.
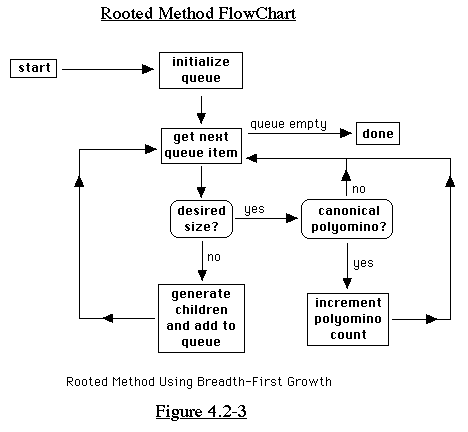
4 Sequential Enumeration
The most straightforward way to enumerate polyominoes is to somehow
generate all polyominoes (probably more than once each), and check
all rotations and reflections so that we do not count the same
polyomino twice. A simple way to break the problem up into more
manageable pieces is to only search for polyominoes of a certain
size and linesize. This basic method of enumeration is shown in
the flowchart in Figure 4-1.
In the next few pages, we will examine the parts of this flowchart
in detail. Later, we will present a completely different approach
to enumeration.
4.1 Extension Method
In this section, we will describe the extension method of generating
polyominoes, a method which follows the flowchart of Figure 4-1.
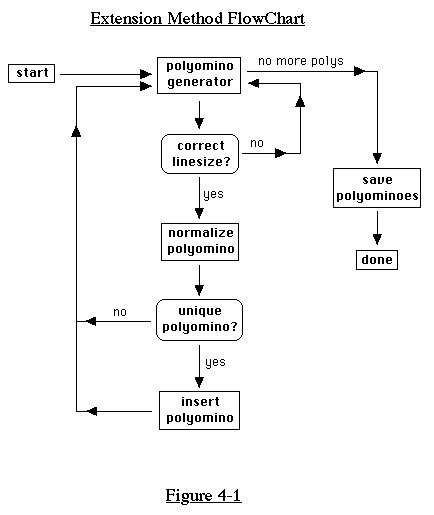
4.1.1 Generating Polyominoes
To enumerate the polyominoes, we must find a way of generating
them in a way which guarantees completeness. We want to find a
method to generate all the polyominoes, but with as few repetitions
as possible.
Choose Squares
A naive way of generating polyominoes of size n is to choose n
squares (checking for connectedness) from an n by n grid. This
is straightforward and certainly complete, but there is too much
repetition. n*n choose n grows almost as fast as (n*n)! does.
Move List
A better way is to create polyominoes by starting from one corner
of the grid, and moving from square to square, marking all squares
we touch. If we number each move based on direction (0 = up, 1
= left, etc.) then we generate a complete set of polyominoes which
is easily enumerated. This is better than the choose method, but
still results in quite a bit of repetition. This method grows
as 4^m, where m is some number larger than n (this depends on
backtracking).
Extension Method
Another method would be to take the size 'n-1' polyominoes, and
extend them by adding one square, to get a size 'n' polyomino.
(See Figure 4.1.1-1) The extension method was noted by Golomb.
[Gol65]
To form a size n polyomino from a size n-1 polyomino, we can add
a square in roughly 2*(n-1) places. This is a good rough estimate
because most squares in a polyomino are attached in at least 2
places. So, for each of the n-1 polyominoes, there are about 2
places to put extra squares. Thus, to find size n polyominoes,
we need to look at (# size n-1 polys)*2*(n-1) different polyominoes.

Intuitively, this is clearly better than the move-list method
because by building on top of smaller polyominoes, we retain some
information. In practice, the extension method is indeed much
better than the move list method. This will be shown later in
the performance section.
The only problem with the extension method is that to calculate
p(s,l) (number of polyominoes with size s, linesize l), we must
first compute p(s,i) for all i < l. So we must save the polyominoes
to a file for future use.
In general, the move-list method can be improved by avoiding redundant
cases, but this requires special-case programming. The extension
method is a fundamentally better method of generating the polyominoes.
Note that the extension method could also be improved, since we
don't have to check all squares if the smaller polyomino has symmetry.
However, the cost of checking for symmetry probably outweighs
the potential gain in speed. In fact, as is evidenced by Lunnon's
results, and proven theoretically, the number of polyominoes with
no symmetry divided by the number of polyominoes approaches 1
as the size of polyominoes grows larger.
4.1.2 Hashing
One of most fundamental tasks of the polyomino program is to support
uniqueness. We have to ensure that a polyomino has not already
been counted. To do this, we store all of the unique polyominoes
in a hash tree/table structure, and compare the candidate polyomino
with only a small subset of the unique polyominoes. To access
the hash structure, we first branch on some criteria(on) to find
the correct hash table, then index into the hash table.
If we compare the candiate polyomino only with polyominoes of
the same height and width, this narrows down the search considerably.
We can also branch on the y-coordinate of the last square. This
seems a bit strange, but it works well. (See Figure 4.1.2-1) To
narrow it down even further, we use a hash function. This takes
the XOR of every n bits, where n = height-1. (See Figure 4.1.2-2)
This is not necessarily the best hash function, but it is simple
to implement, and gives fair results, as we will see.
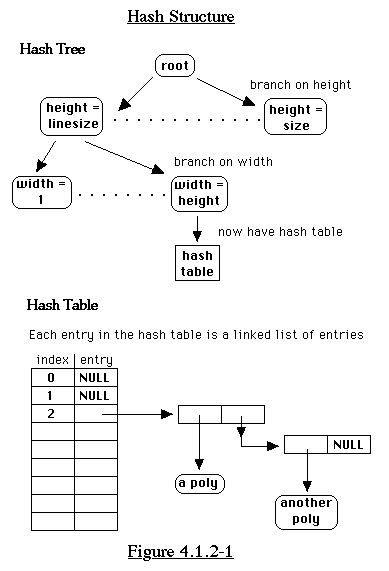

Criteria for branching
A branching is good if there are guaranteed to be polyominoes
going to every
branch. This ensures a minimization of wasted space. As more branches
are
used, the hash tables can be made smaller to avoid using too much
memory.
A branching is ideal if the branching separates the polyominoes
into groups of equal size. Clearly, if every leaf of the tree
corresponded to a single polyomino, this would be ideal.
A branching is good if it has many branches. The more possibilities,
the better. If each branch has exactly 'p' possibilities, then
we need log (base p) of n (where n = number of polyominoes) branchings
for complete separation (without using a hash table). As p grows,
this number gets smaller. Thus, the computation time needed to
figure out where a polyomino goes becomes smaller.
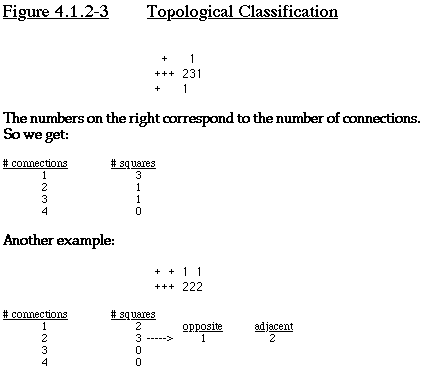
Topological Classification
One possible branching scheme is to use some sort of topological
classification. We can classify squares of a polyomino by how
many other squares it is adjacent to; we can classify the polyomino
based on the number of squares adjacent to 1, 2, 3, or 4 other
squares. As a further branch, we could distinguish between squares
adjacent to 2 other squares those where the adjacent squares are
on opposite sides, and when they aren't. See Figure 4.1.2-3 for
an example of topological classification.
Evaluating Hash Functions By Classification
To evaluate some hash functions, we can classify the polyominoes.
By
classifying the 4655 size 10 polyominoes, we are able to get a
rough idea
of how a given hash function would perform. This has been done
and the results are listed in Appendix A.
From the results, it is clear that the topological classification
described above is not a good hash function. For size 10, there
are up to 10^4 = 10000 possible branches for topological classification.
Howevever, less less than 50 of these are filled. And out of 4655
polyominoes, 1273 belong to the same branch. This is over 1/4th
of the total! Clearly, the amount of calculations required to
do topological classification do not justify the inefficient branching.
The hash function described in Figure 4.1.2-1, however, is much
better. No more than 369 of the 4655 polyominoes belong to the
same branch, and more of the entries are filled. Also, note that
topological classification is an expensive operation, while height
and width are easy to compute (besides, they are needed for normalization
and are desirable in computing rotations). So this hash function,
while not perfect, is the one we will use.
4.1.3 Storing Polyominoes For Uniqueness Check
One interesting question is which polyominoes we should store
for the uniquness check. This section addresses that question.
Normalization
One thing we can do to normalize a polyomino is to only store
it if its height is greater (or equal to) its width. Clearly,
this allows us to still count all polyominoes. On the other hand,
because of this restriction, we don't have to bother with comparing
certain rotations or reflections of that polyomino. Because checking
that height >= width is a simple, quick operation, we end up saving
some time. (Note that we don't gain anything, though, if height
= width, in which case all rotations/reflections have that same
property.)
Storing Rotations
One interesting question is whether or not we should store all
1, 2, 4 or 8 rotations of a unique polyomino. If we do store them,
then we only have to make one comparison for every polyomino we
check. If we don't, then we have to compare up to 8 rotations.
There are two disadvantages to storing rotations. First, there
is the obvious disadvantage that it takes up to 8 times as much
space. Secondly, however, it affects hashing. We are cramming
8 times as many objects into the hash structure. So this will
affect performance of the hash structure. In fact, it may offset
almost completely the supposed speed-up.
So, in summary, storing the rotations will probably cause no significant
speed-up, but will use up to 8 times as much space.
As we will see later in the section on parallel algorithms, checking
all rotations can be avoided by using canonical polyominoes.
4.1.4 Data Structures
There are several possible ways to store polyominoes. When we
first
check a polyomino, we want to be able to rotate and reflect it
with ease,
be able to hash it, and also compare it with other polyominoes.
The one
data structure that fulfills these requirements is a simple array.
Array
For a size n polyomino, simply use an nxn array, with 0's for
empty
squares, and 1's for filled squares.
Pros: easy to compare two polyominoes of this format; easy to
flip, rotate polyominoes; easy to hash (find height, width, etc.)
Cons: slow to compare (order n*n); takes up a lot of space
Once we determine a polyomino is unique, we don't need to perform
any
transformations on it. The only requirement is that it is easy
to compare
with polyominoes stored in the array format. Also, its size should
be kept
to a minimum, since there are many of these polyominoes at any
one time.
The data structure which best fits these requirements is a square
list.
Square List
This is an array consisting of the (x,y) coordinates of the filled
squares.
Pros: doesn't take up much space (2*n integers); fast and easy
to compare polyomino in this format with polyomino in array format
(n comparisons)
Cons: hard to compute hash functions
4.2 Rooted Translation Method
The extension method is good, but it suffers from the inherent
problem of requiring good performance of the hash table.
Rivest suggests a different method which is fundamentally different.
Rivest describes a method to generate rooted translation type
polyominoes. [Kla81]
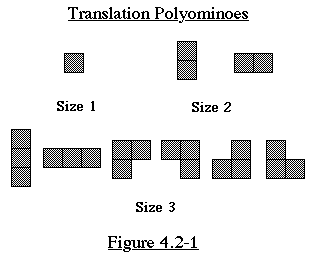
The translation type polyominoes of size n are the size n polyominoes
and their rotations/reflections. (Any two translation polyominoes
are alike if and only if they can be translated to be equivalent)
See Figure 4.2-1 for some examples of translation polyominoes.
A rooted polyomino is a polyomino where one of the squares is
designated a root.
Rivest's method allows us to find the all the rooted translation
type polyominoes of any size without making any comparisons . This is what makes this algorithm so fundamentally different.
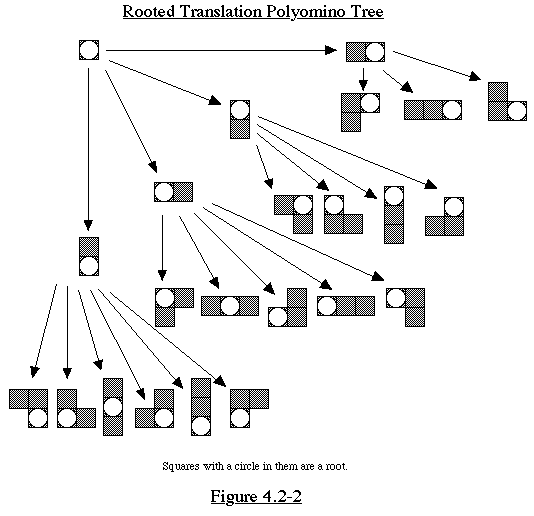
The Rivest method works as follows. We build a tree of polyominoes
in which each parent has as children the rooted polyominoes of
one size greater found by adding a square to the parent. The root
of the tree is the rooted translation polyomino of size 1: a single
square which is also the root. We number that square 0. Now, we
number the surrounding squares 1, 2, 3, and 4. The children of
the root are the 4 polyominoes created by placing a square in
one of those numbers. For each parent, we find all the children
as follows:
- Number all unnumbered squares adjacent to the parent polyomino
with the numbers directly following any already used in this polyomino.
- The children are the polyominoes made by placing a square on
one of those numbers with the condition that any new square
must be numbered greater than anything already in the parent
polyomino. This requirement avoids redundancy.
At level n of the tree, we have all the size n rooted translation
polyominoes
exactly once each. Say there are m of these. Since each translation
polyomino
corresponds to n different rooted translation polyominoes (root
in any of the n squares), there are m/n rooted translation polyominoes.
(See Figure 4.2-2)
We can use this method to find the polyominoes of size n as follows.
First, we find the rooted translation type polyominoes. Then,
we can choose only those polyominoes in which the root is, for
example, the leftmost square on the bottom of the polyomino. Then,
as we will describe later, we can choose only the canonical form
polyominoes to disregard rotations. In this manner, we can find
all the polyominoes of size n without making any explicit comparisons.
(See Figure 4.2-3)
Basically, using rooted polyominoes is similar to the move-list
method, but with a more coherent, regulated approach. The fact
that it doesn't require any explicit comparisons makes it very
attractive.
4.2.1 Tree Growth: Depth-First vs. Breadth-First
There are basically two different ways of growing the tree of
rooted translation polyominoes. It can be grown either depth-first
or breadth-first.
Breadth-first growth can be implemented using a queue. We start
with a queue with only the size 1 rooted translation polyomino.
Each time, we take one polyomino from the queue, and add its children.
The problem with the breadth-first approach is that the queue
gets very large very quickly. Lunnon's results tell us that at
size 8, there are 2725 rooted translation polyominoes, and at
size 12 there are 505861. As has been shown, there are roughly
8 times as many rooted translation polyominoes as polyominoes.
The memory required would force our search to stop at small sizes.
Depth-first growth can be implemented using recursion. If we write
a procedure Grow() which takes a parent polyomino and finds its
children, then we can write it in this manner:
Grow(parent )
for ( all children child of parent )
Grow(child )
This takes advantage of the fact that after we reach the end (we
reach
the size we want), we don't need to keep that polyomino anymore.
We just
note it, then backup and continue. At any one time, we only need
to keep
n polyominoes in memory, where n = size of polyominoes. This solves
the problem presented by the breadth-first growth.
4.2.2 Three-Dimensional Polyominoes
Any of the algorithms which produce 2-dimensional polyominoes
can be extended to produce 3-dimensional polyominoes. However,
we will just examine using the rooted method to find 3-dimensional
polyominoes.
The only major change that needs to be done is to modify the program
to take into account all 24 (or 48) orientations, as opposed to
the 8 two-dimensional orientations.
The only problem with finding three-dimensional polyominoes is
that it is hard to print them out. While the two-dimensional programs
can produce easy-to-see polyominoes, the three-dimensional ones
can only produce crude 2-d views from 3 different angles. Future
versions of the program could take advantage of X window graphics
capabilities.
4.3 Performance
In the following pages we will compare the various methods of
enumeration running on a sequential machine.
The next three sections will examine the performance of the extension
method. The third and fourth will look at the rooted method, with
the fourth section also comparing the extension and rooted method
against each other.
4.3.1 Hash Structure Performance
We first examine the performance of the hash structure used in
the extension method. The hash structure is used to reduce the
number of identity checks we have to make (when we compare a polyomino
for uniqueness). So, we would like to know how many checks are
actually made.
The numbers in the following table are depth/rotations checked.
This is the average number of polyominoes checked for each rotation.
For example: Given a polyomino with no symmetry, we have to compare
all 8 of its orientations against the hash structure, each orientation
being compared against some subset of the hash structure. If each
of those is checked against 2 entries in the hash structure (16
total comparisons), then the average depth/rotation is 2.0. (Note:
LS is linesize)
| Line Size |
8
|
9
|
10
|
11
|
12
|
13
|
|
3
|
0.444 |
0.575 |
0.901 |
1.319 |
2.047 |
3.241 |
|
4
|
0.480 |
0.975 |
1.876 |
3.668 |
7.465 |
16.145 |
|
5
|
0.313 |
0.519 |
1.091 |
2.609 |
6.758 |
17.852 |
|
6
|
0.092 |
0.325 |
0.530 |
1.123 |
2.716 |
7.270 |
|
7
|
|
0.231 |
0.317 |
0.528 |
1.119 |
2.774 |
|
8
|
|
|
0.107 |
0.336 |
0.546 |
1.105 |
|
9
|
|
|
|
0.133 |
0.325 |
0.538 |
|
10
|
|
|
|
|
0.116 |
0.345 |
|
11
|
|
|
|
|
|
0.137 |
Table 4.3.1-1 Hash Depth/Rotation
As you can see, the numbers get larger as the number of polyominoes
grows.
The worst performance is for linesizes 4 and 5 which classifies
most of
the polyominoes for these sizes. We would like the performance
to be constant, even as size grows, but this is not the case for
this hash structure. Perhaps better hash branches and functions
could be created, but this avoids the fundamental problem of having
to use the hash function in the first place.
4.3.2 Extension vs. Move-List
The numbers in the two tables below are the number of polyominoes
checked
for uniqueness. For example, to find the size 8, linesize 3 polyominoes,
the extension method must check 316 polyominoes for uniqueness.
Extension Method
Size
LS 8 9 10 11 12 13
3 316 734 1905 4835 12872
4 444 1911 6930 25485
5 211 909 4459 19608
6 37 323 1538 8271
Table 4.3.2-1 Number of Polyominoes Checked - Extension Method
As stated earlier, the number of polyominoes checked should be
dependent on the number of polyominoes. Comparing this table with
Table 6-1 bears this out.
Movelist Method
Size
LS 8 9 10 11 12 13
3 1890 14178
4 827 6405 87142
5 216 11886
6 19974
7 32488
8 5647
Table 4.3.2-2 Number of Polyominoes Checked - Move-List Method
The numbers clearly show that the extension method of generating
polyominoes is much better than the move-list method. Remember
that in the move-list method, the number checked grows as the
linesize shrinks, whereas the number checked in the extension
method grows as the number of polyominoes. So, for example, it
is easy to see that the number checked for size 12, linesize 3
will be orders of magnitude better using the extension method.
4.3.3 Extension Method Performance
The following numbers are approximate. For more precise figures,
see Appendix B. Times are listed in seconds.
Size
LS 8 9 10 11 12 13
3 1 2 4 12 37
4 1 4 18 78 358
5 1 3 13 68 383
6 1 5 29 161
7 10 58
8 20
9 5
10 1
Total 3 10 40 197 1023
Table 4.3.3-1 Extension Method Performance
As we expected, the running time is closely dependent on the number
of polyominoes checked, which is dependent on the number of polyominoes.
However, the running time grows a little bit faster than the number
of polyominoes. (see Table 6-1) For example, it takes 5.2 times
longer to calculate the number of size 13 polyominoes than it
does to compute the size 12 polyominoes. However, there are 3.75
times as many size 13 polyominoes as size 12 polyominoes. This
faster growth might be due to the hash structure performance (which
becomes worse with size). Also, as there are more polyominoes,
the hash structure takes up more space in memory, probably causing
more page faults.
4.3.4 Rooted Method Performance
Depth-First vs. Breadth-First
size bfg time dfg time
7 0.12 0.07
8 0.46 0.27
9 1.74 0.98
10 6.38 3.70
11 23.82 14.39
bfg = breadth-first growth dfs = depth-first growth
all times in seconds
Table 4.3.4-1 Depth-First vs. Breadth-First Performance
Depth-first growth is faster because it uses a constant amount
of memory. Breadth-first is constantly taking up more memory space,
probably causing a lot of page faults, degrading performance.
Translation Polyominoes vs. Regular Polyominoes
If we are only interested in finding the asymptotic growth of
the number of polyominoes, it suffices to find the number of translation
polyominoes (since the ratio of polyominoes to translation polyominoes
approaches 1/8 as size approaches infinity).
The following runs were performed using depth-first growth.
size translation regular trans/reg
9 0.64 0.98 0.653
10 2.37 3.70 0.641
11 8.87 14.39 0.616
12 33.43 55.82 0.599
13 127.28 219.03 0.581
all times in seconds
Table 4.3.4-2 Translation vs. Regular Polyominoes
Finding translation polyominoes is quicker because we do not have
to check the leaves of the tree for canonicity. As this is a fairly
long operation requiring several rotations, this is a big savings
in time.
Extension Method vs. Rooted Method
Time Time Growth
Size Extension Rooted Extension Rooted
9 0:03 0:01
10 0:10 0:04 3.33 3.78
11 0:40 0:14 4.00 3.89
12 3:17 0:56 4.93 3.88
13 17:00 3:39 5.18 3.92
Times in min:sec. Times are rounded to nearest second.
Table 4.3.4-3 Extension Method vs. Rooted Method
Table 4.3.4-3 shows that the rooted method is clearly superior
to the extension method. The rooted method was about 4 times faster
than the extension method for the sizes we tested. Also, the asymptotic
growth of the running time is better. The running time of the
rooted method is very slightly worse than about 4^n (the base
rises very slightly with increases in size). On the other hand,
the running time of the extension method is worse than 5^n, with
the base rising noticeably with increases in size.
4.3.5 Three Dimensional Rooted Performance
Size Time Growth Trans. Polys Growth
3 0.04 15
4 0.13 3.250 86 5.733
5 0.69 5.308 534 6.209
6 4.27 6.188 3481 6.519
7 29.00 6.792 23502 6.752
8 3:39.29 7.562 162913 6.932
9 25:26.73 6.962 1152870 7.077
10 2:54:11.85 6.845 8294738 7.195
All times using depth-first growth.
Times in hours:minutes:seconds.hundreths
Table 4.3.5-1 Performance of 3-D Rooted Method
As with the 2-dimensional case, the running time for the 3-d case
is
dependent on the number of polyominoes (Table 4.3.5-1 lists the
number of 3-d translation polyominoes). However, since the asymptotic
growth for 3-d polyominoes is greater, so too is the running time
for the 3-d case. Notice that the running time growth seems to
slow down from sizes 8 to 10. The difference is not significant,
so might be explained by slight variations in machine performance.
5 Parallel Enumeration
In this section, we'll first define some basic concepts in parallel
programming. So, this section may be skipped if not needed.
Introduction To Parallel Programming
One way to write a parallel program is to first write a sequential
version, then modify it. The original program should be examined
to see what parts can be run in parallel, and what interaction
is needed between the processors. To illustrate this, we will
use the following example. Suppose Bob is creating a newsletter.
He has to fold, staple, address, and stamp each newsletter. Now
suppose this friends, Alice, Doug, Elaine, Frank, and Grace want
to help, and we have everyone doing complete newsletters.
If there is only one stapler, then no two people can use the stapler
at the same time. They can do everything else in parallel, except
staple. In a computer program, in this situation, a lock is placed on the stapler. If Alice wants to use the stapler,
she takes the lock; noone else can use the stapler because the
lock is unavailable. When she is done with the stapler, she replaces
the lock.
Suppose the addresses are all printed on labels. There are many
different labels, but no two people should use the same label.
To avoid this problem, we could put a lock on the entire label
sheet. This would work, but is a little bit of overkill since,
for example, Doug and Elaine should be able to take two different
labels at the same time. This is the problem of concurrent queues.
There are some simple solutions to this problem. For example,
we can tear the label sheets into equal parts so that each person
is responsible for a certain subset of the addresses.
The above solutions to concurrency problems involve shared memory
in which all the processes share the same memory. This is not
always possible, however, depending on the hardware. A different
set of solutions involves message passing. For example, when Frank
picks up the stapler he can say Ive got the stapler. Everyone
else will hear that and knows that the
stapler is unavailable. When Frank is done, he can say I'm done
with the stapler.
This has all been very democratic where every process is equal.
We could also have a single master process and several slave processes.
For example, Grace could be in charge of assigning duties and
gathering the completed newsletters. She could tell Alice to fold,
Bob to staple, Doug and Elaine to address, and Frank to stamp.
Or at any moment tell Alice to stop folding and help Frank stamp.
Basically, a master process is only really useful if there is
a lot of complex interaction between the different processes,
or if many processes are needed to do the same thing, but one
process is needed to do something completely different.
One way to avoid all these problems with process interaction is
to change the existing algorithm to avoid as much interaction
as possible. This is desirable as long as the underlying running
time of the new algorithm is not substantially slower than the
original one. For example, we can organize it assembly-line style,
with each person doing a different job. However, some jobs take
longer than others and someone may end up sitting around with
nothing to do much of the time.
One important feature of the newsletter problem is that we don't
care in what order the newsletters are done, as long as they're
all done in the end. As long as we can keep this property, we
can get good performance. If not, however, then we will be forced
to do things in a certain order and may lose precious time.
5.1 Extension Method
The extension method can be parallelized in a rather straightforward
way.
The extension method basically involves taking a polyomino generated
using extension, and then comparing it with polyominoes in a hash
structure. To accomodate this in the parallel version, we can
read all the smaller polyominoes in from a file, and store them
in a queue residing in shared memory. Each process takes an item
from the queue and checks it with the hash structure, which must
also reside in shared memory. This is one of the inherent problems
with parallelizing the extension method -- it requires a lot of
shared memory. (See Figure 5.1-1)
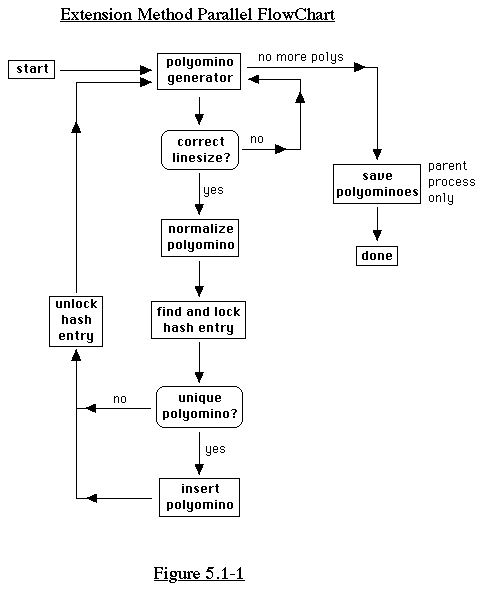
Still, we can generate good performance through an understanding
of the problems of shared memory. We discuss these problems in
the next couple of sections.
5.1.1 Locking The Hash Structure
When a process checks a polyomino for uniqueness, it must not
allow anything to interfere with it. In other words, it cannot
let another process insert a polyomino which might be the same
(modulo reflection or rotation) as the one it's checking. Thus,
before beginning to check for uniqueness, a process should lock
the portion of the hash structure in which such a polyomino could
be inserted. When it is done checking, it inserts the polyomino
if appropriate, then releases the lock.
Of course, using a lock on the hash structure has its problems.
It is akin to having only one stapler. Most of the time, Alice
will be folding or licking stamps or watching the person next
to her. But she will need to use the stapler, and sometimes it
won't be there. She could start the next newsletter while waiting,
but she'll have to keep track of which newsletters she's stapled
and which she hasn't. This is possible, but it's easier to just
buy more staplers. We can't do that with the hash structure, but
we can split it up into parts and lock only the parts, since each
process doesn't need to use the entire hash structure at any one
point.
The smaller the parts we have to lock, the better. As the parts
get smaller, the probability that two processes have to access
the same part at the same time is smaller. Thus, the processes
spend less time waiting for each other.
Independent Branches
Because we require that height > width, height and width are independent
of reflection and rotation. Thus, we can get away with locking
only the part of the structure in the appropriate height/width
branch. This is better than locking the entire structure, but
can be improved. To get better performance, we can try to lock
a smaller portion by finding rotation/reflection independent branches
other than height and width.
One such branch that might be used is the topological classification
described earlier. However, it was shown that this is not a good
branch in general.
There don't seem to be that many good hash branches, but something
is definitely needed. This is clear because the performance of
the hash table becomes worse for larger polyominoes. In one run
of the sequential version, there was an average depth of 17 polyominoes
per entry.
Canonical Polyominoes
We could try to find more rotation/reflection independent branches
to use, but this avoids a fundamental problem. Why do the branches
have to be rotation/reflection independent? Because when we check
for uniqueness, we check all rotations/reflections. But what if
we find a way to express all rotations/reflections of the same
polyomino as a single polyomino? Then we only check a single polyomino
and the branches do not have to be rotation/ reflection independent.
Lunnon provides just such a polyomino when he describes a canonical
polyomino. [Lun71] He numbers the squares in a standard ordering,
and specifies a polyomino by listing the square numbers in order.
The canonical polyomino is the rotation/reflection which is first
in alphabetical order (if the square numbers were letters). This
is exactly what we want. We store only canonical polyominoes,
and check canonical polyominoes for uniqueness. See Figure 5.1.1-1
for an example.

This has the very pleasing side-effect of removing a lot of calculation
from the critical section (section where a process has the lock
to something). To calculate the canonical polyomino, we have to
rotate/reflect it. But we can do this before locking the appropriate
section of the hash table. Before, we had to rotate/reflect the
polyominoes while checking for uniqueness. Thus, a process spends
less time doing calculations while it has a lock.
Now that we do not need rotation/reflection independent branches,
we don't even have to lock hash tables we can lock individual
hash entries. Once we find the canonical polyomino, we know exactly
where any duplicate will be inserted, and can lock it.
Lunnon goes on to describe an improved version of canonicity.
A polyomino is canonical if its center of gravity is safely inside
a fixed eighth of its bounding rectangle. If its center of gravity
is on the edge, then we must revert to the old check. This version
of canonicity is supposed to reduce the amount of computation
required to determine canonicity. However, it is not clear that
this is so (computing center of gravity is not a blindingly quick
task), and we do not use this method.
5.1.2 Announcement Board
There is other methods of solving the problem of conflicts in
the hash structure. When two processes both want to access the
same part of the hash structure, this only causes problems if
the two polyominoes they are comparing are the same, and not yet
in the hash structure.
One way to take advantage of this fact is to use something we'll
call an announcement board. Each process has two slots in the
board one for a pointer to the part of the hash structure it is
using, and one for a pointer to the polyomino it is comparing.
When a process wants to use a part of the hash structure, it fills
its two slots in the board, and goes ahead and uses the hash structure
(without waiting for other processes to finish). If the polyomino
is not unique, it simply moves on to the next polyomino (it should
probably erase its slots first, while it gets the next polyomino).
If instead the polyomino is unique according to the hash structure,
it must check the other processes. It looks at the announcement
board. If it finds a process which is using the same part of the
hash structure, it compares its polyomino with the one corresponding
to that slot in the board. If it is the same, the process throws
away its polyomino (and lets the other process count it) and clears
its slots in the board. Note that the announcement board itself
should be locked when this is done, or both processes may throw
away the polyomino (meaning it isn't counted at all).
The announcement board is one method of resolving conflicts. However,
it is best used when there are bound to be a fair number of conflicts.
If there aren't a lot of conflicts, then the overhead of maintaining
the announcement board may override any time otherwise saved.
Because the canonical approach guarantees few conflicts, we do
not use the announcement board, but present it here as an alternative
where canonicity is not an option.
5.2 Rooted Translation Method
The rooted translation method can also be transformed into a parallel
program.
In Section 4.2.1, we compared breadth-first growth and depth-first
growth, coming to the conclusion that depth-first is better. Unfortunately,
it is not immediately clear how to go about parallelizing depth-first
growth. There appears to be no real way to split up a recursive
procedure with only one recursive call to itself.
Fortunately, breadth-first growth allows us this separation. We
can grow the rooted translation tree to a suitable depth, then
grow the rest of the tree using depth-first growth.
Once the tree has been grown using breadth-first growth, the nodes
are in a queue in shared memory. Each process takes one of those
nodes and grows all its children using depth-first growth. When
it is finished, it goes to the queue for another, until none are
left (the whole tree has been grown).
Thus, with only a small start-up sequential time (to grow the
first few
levels using breadth-first growth), we are able to keep the same
general performance of using depth-first search. Note that because
we need not compare the generated polyominoes with any hash (or
other) structure, there is no interaction between the processes
other than the queue of nodes grown by breadth-first search. There
are no other locks. So there is very negligible amount of time
spent waiting for other processes.
The only question that remains is: How deep should the breadth-first
growth go? This depends on the number of processes being used.
Clearly, if more processes are used, then the depth should be
greater. If 15 processes are used, and only 6 nodes are generated
using breadth-first search, then 9 of the processes will lie around
with nothing to do. If 15 processes are used, and 19 nodes are
generated using breadth-first search, then once the first 15 nodes
are finished, the remaining four will be taken by 4 processes,
while the other 11 processes remain idle. But clearly, if 2725
nodes are generated using breadth-first search, then the difference
in work done by each of the 15 processes would be negligible.
The exact differences in performance will be discussed in the
performance section.
5.2.1 Three-Dimensional Polyominoes
The parallelization of the 3-d rooted translation program is basically
the same as that of the 2-d program.
Because of the larger amount of memory needed, however, there
were problems getting the 3-d program to work. When multiple processes
are used, the machine does not allow local (not shared) dynamic
memory allocation greater than 16 kilobytes. This is not enough.
To allow for sizes up to 16, a single 3-dimensional polyomino
needs 16 kilobytes (16x32x32). Depth first growth needs dynamic
memory allocation to grow the different nodes, but it only uses
a constant amount of memory at any one time. In fact, it allocates
and frees memory in a stack-like fashion. This meant it was easy
to write a short package to allocate memory from a fixed (static)
block of memory.
5.3 Performance
It should be noted that all parallel runs were done on a different
machine than the sequential runs (section 4), so no comparison
can be made between the two.
In looking at the data on the next few pages, keep in mind that
the nature of parallel processing means most of these numbers
are approximate.
5.3.1 Extension Method Performance
Because of the large number of different runs that would be required
to test every combination of size, linesize, and number of processors,
we will only examine a few tests.
First, we will look at the performance of 12 processors. Then,
we will take a few size/linesize combinations and compare performance
for different numbers of processors.
Run Time Speedup
Size LS Seq. Time 12 procs. 1 proc. Actual Parallel
11 3 12.1 15.2 41.1 2.70 9.35
11 4 14.0 26.3 141.3 5.37 10.35
11 5 13.8 23.4 107.5 4.59 9.76
12 3 27.3 35.9 115.9 3.23 10.30
12 4 35.9 84.9
Table 5.3.1-1 Performance of 12 Processors
Sequential time is the amount of time used to read in the small
polyominoes and the time to print out the results. This is the
time when only one process is active. Values are very approximate.
The actual speed-up refers to the speed gained by comparing actual
run times. The parallel speed-up refers to the speed-up of the
parallel portion of code. For example, examine size 11, linesize
3. The actual speed-up is 41.1/15.2 the ratio of the run times.
But about 12.1 seconds of the run time is taken when only one
process is active. So the parallel speed-up is (41.1-12.1)/(15.2-12.1).
The parallel speed-up of about 9 to 10 times is close to the desired
12. However, a large percentage of the run-time is done sequentially,
causing the actual speed-up to be disappointingly low (about 4
times).
The relatively large sequential time is an inherent problem of
the extension method. The parallel speed-up is probably not exactly
12 because of locking the hash table. It is close, but perhaps
using an announcement board (as described in Section 5.1.2) would
help. It would be interesting to see if this improved the parallel
speed-up much.
In the rest of this section, we will examine the performance on
tests of size 10, linesizes 3-6.
Size Linesize Time
10 3 5.0
10 4 5.4
10 5 5.4
10 6 4.9
Table 5.3.1-2 Sequential Time For Size 10
Because the sequential time skews results so much, we'd like another
measure of performance (parallel speed-up is one, but requires
a bit of computation). One such measure is CPU time. This is the
total amount of CPU time taken by all the processes. This gives
us a better idea of how much time is spent waiting for locks.
Number of Processes
Size LS 1 2 3 4 6 8 12
10 3 13.0 13.1 131 13.3 13.5 13.8 14.9
10 4 33.2 33.6 34.0 34.4 35.2 36.6 37.7
10 5 21.7 21.9 22.9 22.6 22.8 23.1 23.7
10 6 9.1 9.5 9.5 9.7 9.8 10.0 10.2
Table 5.3.1-3 CPU Time
Very little extra CPU time is used. Between 9 and 15 percent extra
CPU time is used in these tests. This is not much, but it will
degrade performance. For example, even with no sequential time
and perfect distribution of CPU time, the best speed-up possible
of size 10 linesize 4, 12 processors is 33.2*(37.7/12) = 10.57.
(Note: the CPU time was fairly evenly distributed, with the average
deviation per process being less than 0.1 seconds)
Number of Processes
Size LS 1 2 3 4 6 8 12
10 3 15.2 10.3 8.7 8.1 7.2 6.8 6.5
10 4 35.6 21.3 16.6 14.4 11.6 10.1 9.1
10 5 24.7 14.9 12.9 12.4 9.4 8.2 7.5
10 6 11.4 8.5 7.7 6.9 6.7 6.2 5.9
Table 5.3.1-4 Run Time
Number of Processes
Size LS 1 2 3 4 6 8 12
10 3 1.00 1.48 1.75 1.88 2.11 2.24 2.34
10 4 1.00 1.67 2.15 2.47 3.07 3.53 3.91
10 5 1.00 1.66 1.91 1.99 2.63 3.01 3.29
10 6 1.00 1.34 1.48 1.65 1.70 1.84 1.93
Table 5.3.1-5 Effective Speed-up
The numbers for effective speed-up aren't too exciting. We knew
they were going to be bad. More interesting are the numbers for
parallel speed-up.
Number of Processes
Size LS 1 2 3 4 6 8 12
10 3 1.00 1.92 2.76 3.23 4.64 5.67 6.80
10 4 1.00 1.90 2.70 3.36 4.87 6.43 8.16
10 5 1.00 2.03 2.60 2.76 4.83 6.89 9.19
10 6 1.00 1.81 2.32 3.25 3.61 5.00 6.50
Table 5.3.1-6 Parallel Speed-up
The value for size 10, linesize 5, and 2 processors seems contradictory,
but remember that the sequential time is approximate, and the
values are all rounded.
The parallel speed-up doesn't seem to be very good, especially
compared with the numbers we got for size 11. This could be explained
by a variety of things. We could be under-estimating the sequential
time. More likely, though, is that the runs are too short! They
are too short (in time) to overcome the amount of time necessary
to start up 11 other processes. Starting up a new process takes
time (to copy all non-shared program memory). Even if the processes
take the same amount of CPU time, the performance cannot be ideal
because the processes do not start at exactly the same time (the
original process forks them over one at a time). We could probably
get more useful results if we used a larger size (11 or 12), but
this would obviously take longer.
In summary, the large sequential time leads to disappointing effective
speed-ups. This inherent problem is avoided by using the rooted
translation method, as will be shown in the next section.
5.3.2 Rooted Method Performance
Finding the Right Depth
First, we should find what is the best depth to run the breadth-first
growth before changing to depth-first growth.
The following was done for size 12, running 12 processes.
Depth Nodes Run time Seq time Avg Dev
4 19 49.5 0.1 9.37
5 63 40.3 0.2 2.35
6 216 35.5 0.6 0.57
7 760 35.9 1.9 0.14
Table 5.3.2-1 Comparing Depth of Breadth Growth
Nodes refers to the number of translation polyominoes found at
that depth. The average deviation is the average difference between
the CPU time of a single process and the mean CPU time per process.
Clearly, a depth of 4 won't do for 12 processes. With only 19
nodes, there is too much deviation too much difference between
the amount of work done by each process. The choice is clearly
between a depth of 6 and 7. The sequential time for depth 7 is
slightly larger, which accounts for the running time being slightly
larger. Asymptotically, of course, a depth of 7 will work better.
But we will not run the program for really large sizes, and we
also want to see performance of fewer processes (where the larger
depth is not necessary), so we will use a depth of 6.
Parallel Performance
All of the following runs were done using a sequential depth of
6 (0.6 seconds).
Number of Processes
Size 1 2 3 4 6 8 12
10 27.0 26.9 27.0 27.0 27.0 26.9 27.1
11 103.2 103.1 103.2 103.1 103.5 103.5 103.2
12 397.4 397.4 398.5 398.0 397.5 398.5 399.6
13 1541.3 1542.0 1551.2 1542.8 1547.9 1547.2 1542.2
14 6058.2
Table 5.3.2-2 CPU Time
Accounting for various fluctuations due to machine performance,
there is virtually no different in CPU time for different numbers
of processes. This verifies that there is almost no extra time
spent waiting for the queue (which only has 216 entries).
Number of Processes
Size 1 2 3 4 6 8 12
10 27.5 14.2 9.7 7.5 5.4 4.2 3.2
11 103.7 52.2 35.2 26.5 18.2 14.0 9.7
12 398.0 199.6 133.9 100.5 68.0 51.8 35.5
13 1541.9 771.8 518.1 387.7 262.1 198.1 135.8
14 529.8
Table 5.3.2-3 Run Time
Number of Processes
Size 1 2 3 4 6 8 12
10 1.00 1.94 2.84 3.67 5.09 6.55 8.59
11 1.00 1.99 2.95 3.91 5.70 7.41 10.69
12 1.00 1.99 2.97 3.96 5.85 7.68 11.21
13 1.00 2.00 2.98 3.98 5.88 7.78 11.35
14 1.00
Table 5.3.2-4 Effective Speed-up
This shows that a combination of short sequential time and little
processor waiting adds up to what one would expect very good performance.
The performance seems to get better for increasing sizes. The
larger sizes mean larger running times, making the sequential
time insignificant, and also making the process start-up time
less significant.
We'd like to get a rough idea of what this program could accomplish
given enough time and resources. As a rough estimate, it takes
about 6000 seconds of CPU time to find the 901971 polyominoes
of size 14. This is about 150 polyominoes per second. Given a
65,536 processor machine and 24 hours of real time, we could compute
about 8.5x10^11 polyominoes (850 billion). This means we could
compute the over 650 billion polyominoes of size 24. We'd have
to run the program about 3 days to find the 2.5 trillion polyominoes
of size 25.
5.3.3 Three-Dimensional Rooted Performance
Finding the Right Depth
Again, we should first find what is the best depth to run the
breadth-first growth before changing to depth-first growth.
The following was done for size 7, running 12 processes.
Depth Nodes Run time Seq time Avg Dev
3 15 57.1 0.7 9.96
4 86 44.1 3.4 1.26
5 534 67.0 28.9 0.45
Table 5.3.3-1 Comparing Depth of Breadth Growth
Clearly, a depth of 3 (providing just 15 nodes) is too small.
A depth of 5 is too big for our purposes, because of the large
sequential time. Again, asymptotically it will run better with
a depth of 5, but we aren't going to run the program on really
large sizes. So a depth of 4 is best for our purposes.
Parallel Performance
The following runs wee done using a sequential depth of 4 (3.4
seconds).
Number of Processes
Size 1 2 3 4 6 8 12
6 51.2 54.7 60.5 57.2 57.5 59.0 65.2
7 363.2 379.9 372.8 385.3 396.3 405.1 428.0
8 3113.8
Table 5.3.3-2 CPU Time
Somewhat surprisingly, as opposed to the 2-dimensional case, there
is a noticeable jump in CPU time for the 3-dimensional case. More
CPU time is used for a larger number of processes. Since the only
locks are on the relatively small queue, there aren't many possible
reasons for this disturbing result. The only other link between
the processes is that they start from the same place. Some of
the extra time could be from starting up new processes. This is
a side effect of the solution to the memory allocation problem.
Because each process is using static local memory, all of that
memory is copied from the original process each time a new process
is started. This is something on the order of a quarter to half
a megabyte.
Number of Processes
Size 1 2 3 4 6 8 12
6 53.5 30.4 23.5 17.9 13.2 11.1 9.4
7 365.6 193.0 128.2 100.0 70.5 56.4 42.7
8 275.7
Table 5.3.3-3 Real Time
Number of Processes
Size 1 2 3 4 6 8 12
6 1.00 1.76 2.28 2.99 4.05 4.82 5.69
7 1.00 1.89 2.85 3.66 5.19 6.48 8.56
Table 5.3.3-4 Effective Speed-up
The extra CPU time expresses itself in the form of lower performance.
Again, as with the 2-d case, performance seems to improve for
larger sizes. And again, the same reasons can apply.
6 Results
2-Dimensional Polyominoes
| Line Size |
Size 8 |
Size 9
|
Size 10
|
Size 11
|
Size 12
|
Size 13
|
|
2
|
1
|
1
|
1
|
1
|
1
|
11
|
|
3
|
92
|
222
|
528
|
1330
|
3327
|
8486
|
|
4
|
171
|
574
|
1974
|
6511
|
21636
|
71315
|
|
5
|
75
|
339
|
1381
|
5591
|
21839
|
84140
|
|
6
|
25
|
111
|
557
|
2473
|
10928
|
46329
|
|
7
|
4
|
33
|
167
|
880
|
4159
|
19237
|
|
8
|
1
|
4
|
41
|
230
|
1323
|
6648
|
|
9
|
0
|
1
|
5
|
51
|
319
|
1938
|
|
10
|
0
|
0
|
1
|
5
|
61
|
417
|
|
11
|
0
|
0
|
0
|
1
|
6
|
73
|
|
12
|
0
|
0
|
0
|
0
|
1
|
6
|
|
13
|
0
|
0
|
0
|
0
|
0
|
1
|
|
Total
|
369
|
1285
|
4655
|
17073
|
63600
|
238591
|
|
Trans Polys
|
2725
|
9910
|
36446
|
135268
|
505861
|
1903890
|
Table 6-1 2-Dimensional Polyominoes
The values for the total number of polyominoes and translationpolyominoes,
shown in Table 6-1, match those published by Lunnon. [Lun71]
3-Dimensional Polyominoes
| Size |
Translation Polys |
3-d rotates
|
4-d rotates
|
|
1
|
1
|
1
|
1
|
|
2
|
3
|
1
|
1
|
|
3
|
15
|
2
|
2
|
|
4
|
86
|
8
|
7
|
|
5
|
534
|
29
|
23
|
|
6
|
3481
|
166
|
112
|
|
7
|
23502
|
1023
|
607
|
|
8
|
162913
|
6922
|
3811
|
|
9
|
1152870
|
48311
|
25413
|
Table 6-2 3-Dimensional Polyominoes
The numbers under 3-d rotates are the polyominoes where only 3-dimensioal
rotation is used to check for uniqueness. The column 4-d rotates
refers to those checked with 4-d rotations (3-d rotates and reflection).
The values for up to size 6 match those published by Lunnon. [Lun72]
7 Conclusion
We have evaluated different methods of enumerating polyominoes,
and shown how they can be adapted to parallel processing. We have
described and used an implementation of the rooted translation
method which is almost perfectly parallelizable. It has almost
no sequential time, and almost no conflict between processes.
The method also uses constant memory, leaving time as the only
obstacle to enumerating larger polyominoes. Given a machine with
enough processors, and 3 days, we could enumerate the as-yet unknown
number of polyominoes larger than size 24 (based on Redelmeier's
results, 1981). As Klarner has shown, this will allow us to tighten
the bounds for the asympototic growth constant of polyominoes.
We have also shown that very good performance can be achieved
from concurrent hash tables if careful attention is paid to avoiding
as much conflict as possible. But the best performance of all
is achieved with no conflict at all.
Parallel processing is still a growing field. The available computing
power is there to be harnessed, now, though. Some have successfully
used a network in place of a parallel processor. Using packages
sent over the network, the processors can communicate and act
as a parallel processing machine. There is no shared memory, but
algorithms such as the rooted translation method can be modified
to accomodate this.
Hopefully, this paper will provide a introduction to the problems
of parallel programming. As more and more people become aware
of the power of parallel programming, many more feats such as
those of Stiller will become commonplace.
8 References
[Del91] M. Delest. Polyominoes and Animals - Some Recent Results.
Journal of Mathematical Chemistry. V8 N1-3:3-18. Oct. 1991.
[Del84] Delest, Marie-Pierre and Viennot, Gerard, Algebraic Languages
and Polyominoes Enumeration, Theoretical Computer Science 34 (1984)
169-206
[Gar59] Gardner, Martin. Polyominoes in Scientific American Book Of Mathematical Puzzles and Diversions , Simon and Schuster, New York, 1959, p.124-140
[Gol65] Golomb, Solomon W. Polyominoes , Charles Scribner's Sons, New York, 1965.
[Kla67] Klarner, D.A. Cell growth problems. Canadian Journal of
Mathematics 19 (1967) 851-863.
[Kla81] Klarner, David A. My Life Among The Polyominoes in The Mathematical Gardner , 243-262. Wadsworth International, Belmont, CA 1981.
[Lun72] Lunnon, W.F. Symmetry of Cubical And General Polyominoes
in Graph Theory And Computing , Academic Press, London, 1972, p. 101-108
[Lun72-2] Lunnon, W.F. Counting Hexagonal And Triangular Polyominoes
in Graph Theory And Computing , Academic Press, London, 1972, p. 87-100
[Lun71] Lunnon, W.F. Counting Polyominoes in Computers in Number Theory , 347-372, Academic Press, London 1971
[Mad69] Madachy, Joseph, Pentominoes -- Some Solved And Unsolved
Problems. Journal of Recreational Mathematics V2 #3, 1969.
[Par67] Parkin, T.R. and others, Polyomino Enumeration Results,
SIAM Fall Meeting, 1967.
[Rea62] Read, R.C. Contributions to the Cell Growth Problem. Canadian
J. of Mathematics 14 (1962) 1-20.
[SFC91] Computer Figures Out Old Chess Puzzle, San Francisco Chronicle,
29 October 1991. p. A7 (Associated Press)
Other References of Interest
Delest, M. Enumeration of polyominoes using MACSYMA. Theoretical
Computer Science 79 (1991) 209-226.
M. Delest, Generating function for column-convex polyominoes,
J. Combin Theory Ser. A 48 (1) (1988) 12-31.
M. Delest, Enumeration of parallelogram polyominoes with given
bond and site perimeter, Graphs Combin. 3 (1987) 325-339.
Eden, M. A two-dimensional growth process. Proc. 4th Berkeley
Symp. on Mathematical Statistics and Probability, IV (Univ. of
California Press, Berkeley, 1961) 223-239
Harary, Frank, Graphical Enumeration Problems, in Graph Theory
and Theoretical Physics, Academic Press, London, 1967, p. 1-41
(applications to physics)
Klarner, D.A. and Rivest, R.L. A procedure for improving the upper
bound for the number of n-ominoes. Canadian Journal of Mathematics
25 (3) (1973) 585-602
Klarner, D.A. Some results concerning polyominoes. Fibonacci Quarterly
3 (1965) 9-20.
Klarner, D.A. and Rivest, R. Asymptotic bounds for the number
of convex n-ominoes. Discrete Mathematics 8 (1974) 31-40.
Other References (Not Found)
M. Delest and S. Dulucq, Enumeration of directed column-convex
animals with given perimeter and area, Rapport LaBRI, Bordeaux,
no.87-15
M. Delest and J.M. Fedou, Exact formulas for fully compact animals,
Rapport Interne LaBRIE, Bordeaux, no 89-06
Discrete Math 36 (1981) 246-264.
Golomb, Rec. Math Mag. 4,5,6,8 (1962) General Theory of Polyominoes
Journal of C, I, SS: vol. 1 1976, p.1-8.
Publ. Math. Inst. Hungarian Acad. Sci. 5 (1960) 63-95
|