|
Science Fair Project
Kevin Gong
1986
Background Information
As the title suggests, this project deals with chess - more accurately,
chess pieces. For those who haven't learned how the chess pieces
move, or have forgotten, this section describes the moves.
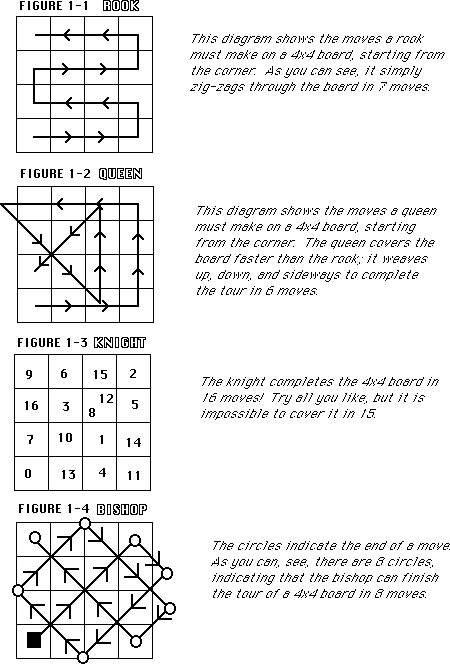
The rook moves only vertically or horizontally (see figure B-1).
The knight moves in an "L" pattern, as shown in figure B-2. The
bishop moves only diagonally, as shown in figure B-3. And the
queen moves as a rook or bishop, as shown in figure B-4.
The king and pawn are not used in this project, so they are not
explained here.
DEFINITIONS OF SOME TERMS USED
Phantom zones - squares which no piece may land on or pass
through
Order-x board - mini chess board with sides of length x
Higher dimensions - geometric dimensions, i.e., not necessarily
time, etc.
PROWL - Programmable Robot Over Whimsical Lanes
Cheating bishop - to cover the entire board, the bishop must be
allowed to move half-spaces, or it will only touch squares of
the color on which it starts
Half-bishop - moves as a regular bishop, but is called a half-bishop
because it only covers half of the board.
Knightship - a piece that moves like a knight, but can move in
the same direction as far as needed - as one move
Purpose
The ultimate goal of this project is to find a formula or formulae
which will show how to solve the following problems.
Imagine a mini-chess board of say, 4x4 units. If a rook is placed
in a corner, how many moves will it have to make before it covers
every single square on the board? And what are the moves themselves?
(See figure 1-1)
How about a queen? To utilize its powers, it should be allowed
to stray off the board; will it accomplish the task faster than
the rook? What if the queen is not allowed to stray off the board? And what about other pieces -
a knight? Or a bishop? (see definition of cheating bishop in section
called Background Information; see figures 1-2, 1-3, and 1-4)
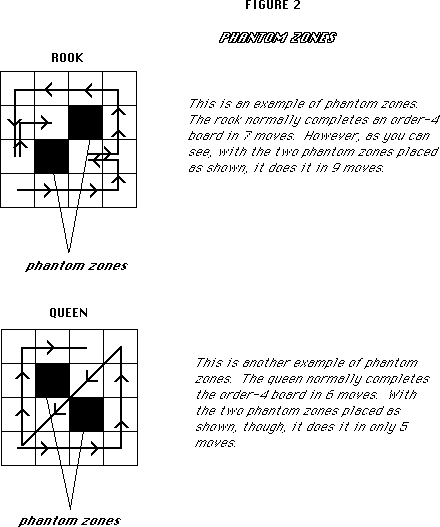
And what will happen if certain squares are designated which no
piece may land on or pass through, called say, phantom squares (see figure 2). What will this do to the number of moves and
the moves themselves?
Another variation is to place the piece on a different starting
square. How will this affect the number of moves?
Remember, we still can try a board of 3x3 units (an order-3 board),
or an order-5 board, or 6, and so on. Finally, what about other
dimensions? What are things like in the 3rd, the 4th, the 5th
dimension?!? And on, and on...
Hypotheses
I expect that the queen will cover the board in fewer moves than
a rook, a rook in fewer moves than a bishop, and a bishop in fewer
moves than a knight. As shown in figures B-1 through B-4, on an
order-5 board the queen can move to 16 different squares, and
the rook, bishop, and knight can each move to only 8 squares.
The knight, however, will always be able to move 8 squares, and will cover only 1 square for every
move it makes. In that respect, then, the knight is inferior to
the other 3 pieces. The bishop should make the route in a greater
number of moves than the rook because to cover the entire board,
it must make half-moves, which increase the number of moves it
has to make.
Phantom zones should change the number of required moves only slightly, if
at all. They do two things. They reduce the number of squares
a piece needs to cover, but they also block the paths to other
squares. These two effects should cancel each other out for the
most part, with differences mainly depending on their placement.
Changing the starting positions of pieces should also change the
results very little. If there is any change, however, it should
make the pieces require more moves. This is because from the corner
everything can probably be covered in a systematic way in few
moves. From any other place, however, the pieces may have to make
strange maneuvers to cover everything, increasing the number of
moves they make.
Method
I wrote several programs in the C programming language (running
on the Apple Macintosh) to test different configurations, i.e.,
different pieces, dimensions, starting positions, and phantom zones.
PROGRAMMING TECHNIQUES
This section gives a brief description of the program structures.
For a more complete description, the folder contains program listings.
The structure behind all of the programs used in this project
is:
Step 1: make a chain of moves
Step 2: simulate the moves
Step 3: skip to another chain and go to Step 2.
During these steps, the program indicates any chain of moves that
completes the tour in a minimum of moves. Step 3 is what determines
the speed of the program, and the one that required the most thought.
This step is in the form of several IF statements, which determine
how far to skip.
Now, consider the length of time a program will have to run in
this way. For example, for a queen on an order-4 board: a queen
can move in 8 different directions, and it must move at least 15 spaces to cover the board. The program, then, must check 815 or about 35,000,000,000,000 different routes!
To remedy this, it was necessary to use many IF statements, i.e.,
Step 3: skip routes. For example, I restricted the queen to not
stray off the board west or south. This greatly reduces the number
of tests to be made.
Results
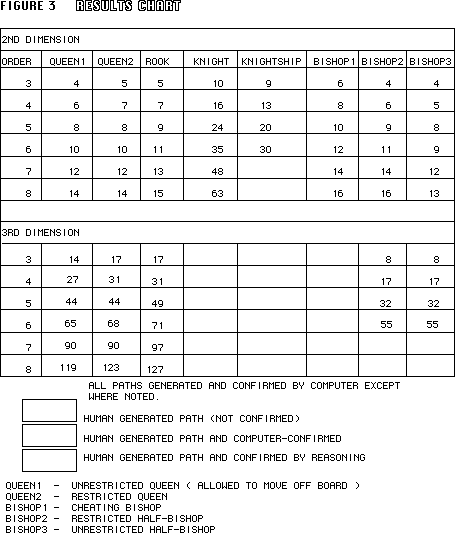
The minimum number of moves for every piece and board size tried
(if a path was found), without phantom zones and starting in the corner, are shown in figure 3. As you can
see, the computer programs did not provide any information for
the higher orders in the 2nd dimension, almost none in the 3rd
dimension, and none in the 4th or greater dimensions. This lack
of information is due to the fact that the amount of time the
programs have to run is enormous. Several numbers obtained from
the computer took over 6 hours to get. And the amount of run-time
increases explosively with higher orders.
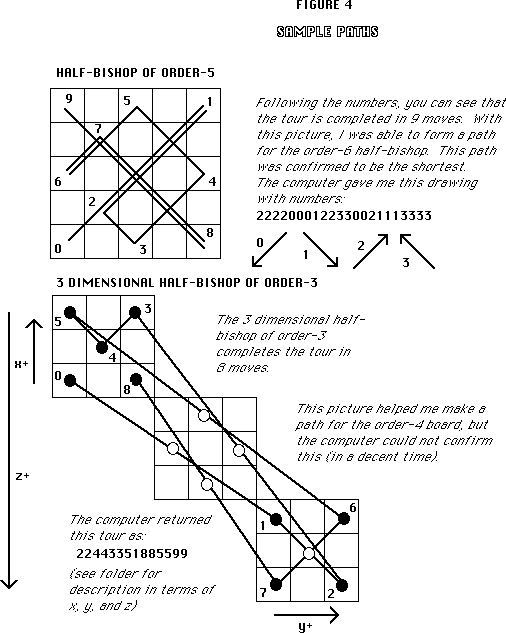
When the programs did give information, however, it did help me
find some short paths. I was able to find paths because I had
the program print out any paths it found in number form, which
I put into drawings. Two examples are shown in figure 4. I was
able to confirm some of the paths with the computer, i.e., it
couldn't find anything better, but most I cannot confirm ( I can't
say I tried every single combination!).
The results for different configurations of phantom zones and starting positions are listed in the folder.
Observations
For the knight, on boards of order-5 and greater, the number of
required moves is simply one less than the number of squares on
the board. This means that the knight is covering the board in
the absolute minimum number of moves, i.e., every move it makes covers a different
square. This seems to be true for all boards larger than order-4.
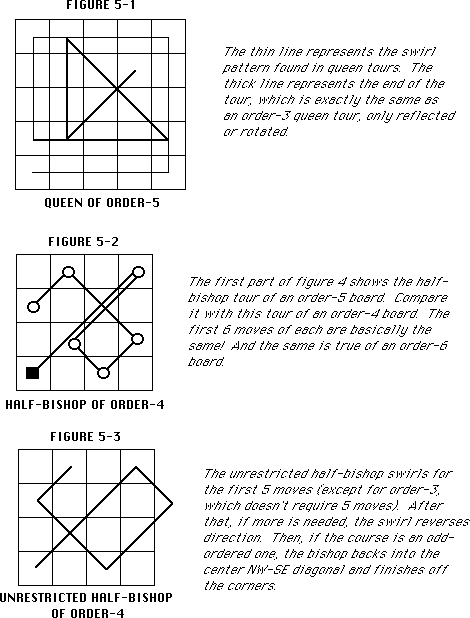
Most of the pieces' moves have visible patterns. For example,
the queen swirls around the center, using only rook moves, and
then finishes off the last 3x3 square with the method used for
an order-3 board (see figure 5-1). The rook also has a pattern
- it simply zig-zags, as was shown before in figure 1-1.
Back in figure 1-4 the complicated pattern of the (cheating) bishop
is shown. It moves in a clockwise semi-swirl. The bishop never
moves in a tight swirl, as can be seen in the picture.
Patterns for the half-bishop and unrestricted half-bishop are
shown in figures 5-2 and 5-3, respectively.
Another observation that can be made is that on boards higher
than order-4, the restricted queen makes the same moves as the
unrestricted queen. On boards of order 3 and 4, the unrestricted
queen has to move off the board to perform the minimum. The restricted
queen, however, cannot do this, and must settle for the rook's
path of a move greater.
Interesting patterns also develop when phantom zones are placed on certain squares or if certain starting positions
are used. The patterns are shown in the folder, under the heading
More Formulas.
Conclusions
In the 2nd dimension, I was able to generate formulas for every
piece I tried except for the knightship. The formulas are all
shown and explained in the section FORMULAS.
As I predicted in my hypotheses, the order of the pieces was as
follows: queen, rook, bishop, and knight, with the queen covering
the board in the fewest moves, down to the knight, with the most
moves.
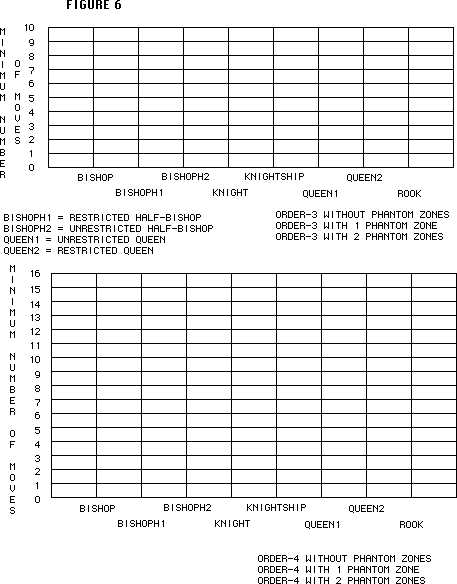
If only one phantom zone is used, my prediction that they do not make a major difference
stands true. However, if two are used, this hypothesis is less
accurate, and could possibly be called wrong. The graph in figure
6 shows the results with and without phantom zones against each
other. As you can see, the phantom zones, on the average, make
the route shorter. This improvement is only slight with one zone, but is more recognizable with two. The folder contains all of
the exact numbers used in the graph.
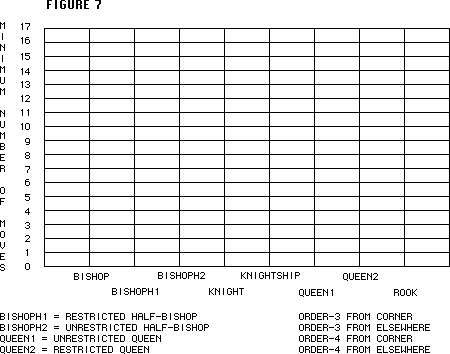
My prediction that changing the starting position will change
the results only slightly is fairly true, as shown in figure 7.
The changing generally results in a longer path, but this is very
slight. The numbers used for the graph in figure 7 are contained
in the folder.
Restricting the queen to the board makes a slight difference in
the smaller orders. In the higher orders, however, the number
of moves are the same as an unrestricted queen. On an order-3
board, the restricted half-bishop requires the same number of
moves as the unrestricted half-bishop. On subsequent higher orders,
however, the restricted half-bishop requires an increasing number
of moves more than the unrestricted half-bishop.
In the 3rd dimension, I was able to generate formulas only for
the rook and unrestricted queen. They are shown and explained
in FORMULAS.
The rook is the only piece that I can generate a general formula
for all dimensions and orders. It is also shown in FORMULAS, along
with its own separate explanation.
Formulas
Deriving formulas varies in difficulty, obviously depending on
the series of numbers. When deriving formulas, it's a good idea
to have a list of the first 10 squares and 10 cubes. That way,
it's easier to spot quadratic or cubic formulas.
If no formula is clear at first sight, extracting differences
may help. For example, at first sight, the series 1, 5, 13, 25,
41, 61 will probably seem a random jumble of numbers. Taking their
differences, however, produces the simple series 4, 8, 12, 16,
20. Since their differences are multiples of 4, we expect the
formula to be n = 4 ( ) + ( ). Seeing this, we can write:
1 = 4 ( 0 ) + 1 The series 0, 1, 3, 6 may not be familiar
5 = 4 ( 1 ) + 1 to some people, but it is known by most
13 = 4 ( 3 ) + 1 people dealing with math to be the sum
25 = 4 ( 6 ) + 1 of the integers 1 to x, or the result of
etc. n = ( x2 + x ) / 2.
So, our final formula reads n = 4 ( x2 + x ) / 2 + 1, x = 0, 1, 2, ...
or n = 2x2 + 2x + 1, x = 0, 1, 2, ...
or n = 2x2 - 2x + 1, x = 1, 2, 3, ...
Wasn't that fun?!
Well, now you know basically how I derived the formulas. These,
then are the formulas:
n = minimum number of moves
x = order of board
int ( y ) = integer value of y. For example, int ( 5.3 ) = 5,
int ( 6.7 ) = 6, etc.
2nd dimension
unrestricted queen n = 2x - 2
restricted queen n = 2x - 2 (when x > 4)
rook n = 2x - 1
cheating bishop n = 2x
restricted half-bishop n = 2x - 4 + int ( ( x + 1 ) / 2 )
unrestricted half-bishop n = x + 2 ( int ( ( x - 1 ) / 2 ) ) -
1
knight n = x2 - 1 (when x > 4)
3rd dimension
queen unrestricted n = 2x2 - x - 1
rook n = 2x2 - 1
General formula for rook
The first two formulas for the rook are 2x - 1 (2nd dimension)
and 2x2 - 1 (3rd dimension). Will 2x3 - 1 be the formula for the 4th dimension? Let's try and find
out. The 3-dimensional order-3 board is completed in 17 moves.
In 4 dimensions, 3 of these need to be covered, which makes 17
x 3 = 51. Adding the two to connect the three "boards", we have
51 + 2 = 53, which equals 2x3 - 1. Therefore, we can assume with almost complete certainty
that the general equation for the rook is nd = 2x(d - 1) - 1, where d is the dimension.
About C
C is a compiled language, which means it is fast. It is also structured,
so that programs tend to be easier to read, and also easier to
edit.
The file input/output is simple to learn, and most of the functions
are similar to Pascal. I had to learn C to write the programs,
so my knowledge of Pascal and the two languages' similarities
helped a great deal.
The quickness, above all else, is why C was the language used.
I said before that the programs were slow, but relative to other
languages on the same computer, they are probably much faster.
Index of Programs
Bishop
2nd dimension P7 - P9
2nd dimension with starting positions P10 - P12
Half-bishop, restricted
2nd dimension P1 - P3
3rd dimension P48 - P51
Half-bishop, unrestricted
2nd dimension P4 - P6
3rd dimension P44 - P47
Knight
2nd dimension P16 - P18
2nd dimension with starting positions P13 - P15
Knightship
2nd dimension P19 - P21
Queen, restricted
2nd dimension P22 - P25
2nd dimension with starting positions P30 - P33
Queen, unrestricted
2nd dimension P34 - P37
2nd dimension with starting positions P26 - P29
Rook
2nd dimension P41 - P43
2nd dimension with starting positions P38 - P40
3rd dimension P52 - P55
More Formulas
When phantom zones are placed on certain squares, and when certain starting positions
are used, there are visible patterns. These patterns are developed
into formulas in this section. For a general explanation of how
the formulas are derived, see FORMULAS.
The formulas are based on a mixture of data, some computer-generated,
and other human-generated.
(ALL FORMULAS ARE FOR 2ND DIMENSION)
WITH A PHANTOM ZONE DIRECTLY ABOVE STARTING SQUARE (CORNER)
Practical Uses
One practical use of this project could be for searching patterns.
If a camera could be instructed, almost as a robot, then this
project could be of use. The camera could be instructed in as
few commands as possible, and then the human can sit back and
look for whatever he's searching for.
Another use could be the programming of robots. If the robot (let's
call him PROWL) can only make 90 degree turns, rook tours will
illustrate the instructions needed to cover all points on a grid,
or something like a grid. If PROWL can only make 45 degree turns,
then queen tours will tell the tale. And if he needs to avoid
obstacles, such as tables, chairs, or buildings, phantom zones will show the way. Figure 8 shows a sample PROWL program.

Why would a robot want to cover all points on a grid? There are
many possibilities. He might be pushing a broom. He might be looking
for something. The robot might be delivering newspapers, or some
other such thing. Or he might simply be taking a walk!
cheating-bishop
n = 2x + 2, x > 3
restricted half-bishop
n = 2x - 4 + int ( ( x + 1 ) / 2 )
unrestricted half-bishop
n = x + 2 ( int ( ( x - 1 ) / 2 ) ) - 1
unrestricted queen
n = 2x - 2
rook
n = 2x - 1
WITH A PHANTOM ZONE IN CENTER (OR AS CLOSE AS POSSIBLE)
unrestricted half-bishop
n = 2x - 2, unless the phantom zone is placed on an unaccessable square, in which case the formula
would be n = x + 2 ( int ( ( x - 1 ) / 2 ) )
restricted queen
n = 2x - 2
unrestricted queen
n = 2x - 2
rook
n = 2x - 2 (if x is even, there are 4 centers, 2 follow the formula,
and the other two follow n = 2x - 1 )
STARTING IN CENTER (OR AS CLOSE TO CENTER AS POSSIBLE)
restricted half-bishop
n = 2x -3 + int ( ( x + 1 ) / 2 )
unrestricted half-bishop
n = 1 + 4 ( int ( ( x - 1 ) / 2 ) )
restricted queen
n = 2x - 1
unrestricted queen
n = 2x - 1
rook
n = 2x - 1
STARTING ON CENTER OF SIDE (OR AS CLOSE AS POSSIBLE)
rook
n = 2x - 1
Proofs that paths exist
This section shows that the paths with the number of moves derived
from the formulas actually do exist. This section does not prove
that they are the minimum - only that they do exist. This section
shows they exist by showing how to get them.
2nd dimension
unrestricted queen
For order-3, the path is simply the last 4 moves of the path shown
in figure 1-2. For higher orders, simply corkscrew rook-wise until
a 3x3 square remains, then finish that off with the order-3 path.
restricted queen
This is the same as the unrestricted queen except for boards of
order 3 and 4, which don't follow the formula.
rook
For any order, simply zig-zag, doing one row, moving up, and so
on. An example is shown in figure 1-1.
cheating-bishop
The cheating-bishop is hard to explain. The best description I
can give is the pattern found in OBSERVATIONS.
In fact, the half-bishop is also hard to explain. It would be
best to look at OBSERVATIONS, which tells you to look at pictures.
It's pretty useless trying to describe it in words.
knight
The knight is hard to show or prove. Finding the knight's paths
for boards larger than order-8 could be a project in itself.
3rd dimension
unrestricted queen
Simply cover a two-dimensional plane of the board using the method
described above, move up to another plane, and repeat until the
"board" (actually, cube would describe it better) is completely
covered.
rook
Same as the 3-dimensional unrestricted queen, except when covering
each plane, uses the rook method.
Possible Extensions
There are several ways in which this project can be extended.
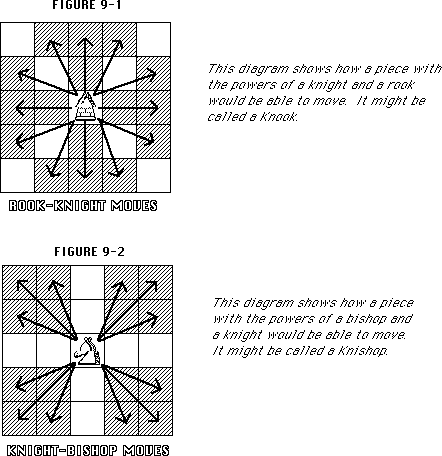
For one, other pieces besides the standard chess pieces can be
used. For example, a piece that can move as a bishop or a knight, or a rook or a knight might be tried (see figures 9-1 and 9-2).
Also, more combinations of phantom zones can be used, or other starting positions. And then, this project
can extend its reaches into more dimensions, i.e., the 4th dimension,
5th dimension, and on, and on...
Here I have only made a scratch on the surface of an almost incredibly
expandable project. The numerous ways to expand this project are
only limited by the imagination.
Figure 4 Description
The numbers used by the computer for the 3-dimensional half-bishop
in figure 4 are as follows:
0 : x = x + 1 and y = y + 1
1 : x = x + 1 and y = y - 1
2 : x = x + 1 and z = z + 1
3 : x = x + 1 and z = z - 1
4 : x = x - 1 and y = y + 1
5 : x = x - 1 and y = y - 1
6 : x = x - 1 and z = z + 1
7 : x = x - 1 and z = z - 1
8 : y = y + 1 and z = z + 1
9 : y = y + 1 and z = z - 1
10: y = y - 1 and z = z + 1
11: y = y - 1 and z = z - 1
|
